
[Python] 백준 알고리즘 온라인 저지 1463 1로 만들기

https://www.acmicpc.net/problem/1463
1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
동적 계획법을 이용해 풀어야 하는 문제로 재귀 같은 경우도 어렵다고 느꼈지만 이번 문제도 어렵다고 느꼈다. 3이나 2로 나눠지면 나누거나 1을 빼서 1로 만드는 최소한의 경우의 수를 구해야 하는 문제였다.
이 문제에서 DP를 사용하는 이유는 이전 경우의 수들의 값을 이용하기 위해 계산결과를 저장하고 그 값을 이용하기 위함이다.
코드
import sys
import math
input = sys.stdin.readline
def dp():
x = int(input())
arr = [0, 0, 1, 1, 2]
for i in range(5, x+1):
one, two, three = math.inf, math.inf, arr[i-1]
if i % 3 == 0:
one = arr[i//3]
if i % 2 == 0:
two = arr[i//2]
arr.append(1 + min(one, two, three))
print(arr[x])
dp()동적 계획법 (Dynamic Programming 이하 DP)
DP는 전역 탐색기법을 활용하여 모든 값들을 계산하여 저장하고 이후 이 값들을 이용하여 문제를 푸는 방식입니다.
DP에는 상향식과 하향식으로 나뉘고 상항식은 제일 작은 값부터 목표 값까지 계산하는 방식이고 하향식은 제일 큰 값에서 제일 작은 값을 향해 재귀를 이용하여 계산하는 방식입니다.
간단한 예로는 피보나치 수열을 예로 들 수 있습니다.
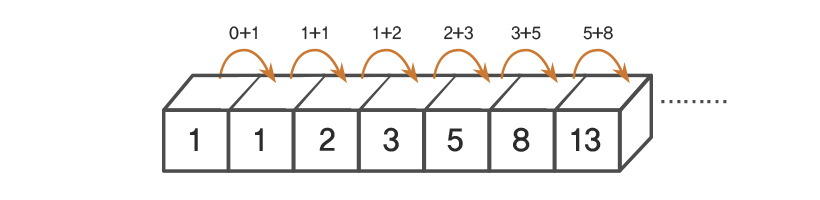
위와 같이 n 값을 구하기 위해서는 (n-1)+(n-2)의 값을 이용해야 하기 때문에 모든 값을 계산할 필요가 있는 것입니다.
풀이
이 문제의 경우 DP의 상향식을 이용하여 작은 값부터 계산하고 그 값을 이용하여 목푯 값을 구하는 방식으로 코드를 작성하였다.
우선 작은 값들은 계산이 필요하지 않으니 정리하면 0 = 0, 1 = 0, 2 = 1, 3 = 1, 4 = 2의 값을 생각할 수 있고 이를 리스트 arr로 미리 선언하고 for문을 이용하여 5번째부터 목표까지 계산되도록 한다.
이후 코드가 조금 복잡하지만 핵심은 3가지 방법을 모두 사용하고 가장 작은 값을 계산된 값으로 리스트에 추가한다는 점과 if문을 통해 줄어든 i를 arr의 값을 이용하여 계산한다는 점이다.
one(3으로 나눠질때 3으로 나눔), two(2으로 나눠질 때 2로 나눔), three(1을 뺌)를 선언한다. math를 import 하여 infinity를 쓴 이유는 최솟값을 구해야 하는데 혹시나 애매한 수여서 겹칠 경우를 방지하기 위함이다.
5를 예로 들자면 5는 3과 2로 나눠지지 않기 때문에 1을 빼야한다. 그럼 4의 최소한의 경우의 수는 이미 알고 있고 1을 뺀 경우 하나만 더 추가하면 5를 1로 만드는 최솟값을 계산할 수 있는 것이다.
else나 elif를 사용하지 않은 것은 모든 if문을 돌며 최소 값을 계산하도록 하기 위함이다. 여기서는 6을 예로 들자면 6은 3과 2 모두 나누는 것이 가능하다. 그렇다면 인덱스 2와 3, 둘 다 1로 값이 같기에 값은 (1+1)이지만 값이 커지면 상황이 달라질 것이다. 이런 식으로 arr 리스트를 목푯값까지 모두 계산해나가다 목푯값(x)까지 계산해 x번째 인덱스를 출력하면 된다.
풀이 결과

'알고리즘' 카테고리의 다른 글
| 백준 11727번 2×n 타일링 2 파이썬 풀이 (0) | 2022.02.11 |
|---|---|
| 백준 11726번 2×n 타일링 파이썬 풀이 (1) | 2022.02.08 |
| 백준 9093번 단어 뒤집기 파이썬 풀이 (0) | 2022.02.03 |
| 백준 10828번 스택 파이썬 풀이 (0) | 2022.01.31 |
| 백준 18870번 좌표 압축 파이썬 풀이 (0) | 2022.01.30 |
